Тема: «Линейное уравнение с двумя переменными и его график».
Тип урока: изучение нового материала.
Вид урока: урок-полилог.
 
Цель:
1. Получить понятие линейного уравнения с двумя переменными, решения уравнения с двумя переменными; познакомиться со свойствами уравнений с двумя переменными; его графиком.
2. Развивать речь, мышление.
3. Воспитывать самостоятельность мышления, любовь к математике.
(Цели учителя: формировать у учащихся способы и средства по освоению понятий и содержания темы. Мотивировать изучение алгебры, как науки, создающей математические модели окружающей действительности.
Помочь учащимся обогатить свой опыт, взглянув на знакомые понятия с различных точек зрения.
Формирование активной, неравнодушной личности.)
Оборудование урока:
Техническое: компьютер, мультимедиапроектор.
Демонстрационное: презентация Microsoft PowerPoint, 3 сосуда. Четыре сосуда: два пустых, два с содержимым и с наклейками «3%» и «30%».
Раздаточное: теоретический справочник, тесты, бланки для построения уравнений.
Ход урока.
1. Организационный момент. - Добрый день. Меня зовут Елена Евгеньевна. Следующие тридцать минут нам суждено с вами прожить вместе.
2. Вступительное слово учителя: - Какой же язык будет помогать нам в общении на сегодняшнем уроке? (язык математики)
- Мне бы хотелось, чтобы у нас сегодня состоялся разговор, ибо как сказал Вовенарг: «Непринужденная беседа — лучшая школа для ума». Хочется еще, чтобы вы помнили слова российского историка Ключевского: «Есть люди, которые умеют говорить, но не умеют ничего сказать. Это ветряные мельницы, которые вечно машут крыльями, но никогда не летают». Надеюсь, что нам сегодня удастся взлететь на вершину новых знаний алгебры.
- Как вы думаете, может ли алгебра понадобиться, например, в парикмахерской? Оказывается, что такие случаи бывают. Послушаем разговор, который там (довольно давно) однажды состоялся.
(Звучит запись разговора):
- Ой, здравствуйте, здравствуйте. Мы слышали, что вы математикой увлекаетесь? - обратился к посетителю один из мастеров. - Не поможете ли нам разрешить задачу, с которой мы никак не справимся?
- Уж сколько раствора испортили для этого! – добавил другой.
- В чем задача? – осведомился посетитель.
- У нас имеется два раствора перекиси водорода: 30-процентный и 3-процентный. Нужно их смешать так, чтобы составился 12-процентный раствор. Не можем подыскать правильной пропорции…
Учитель: - А вы смогли бы помочь эти мастерам?
Задачу можно решить и арифметически. Но язык алгебры приводит здесь к успеху проще и быстрее
Переведем эту задачу с родного языка на язык алгебры:
Возьмем 30-процентный раствор перекиси водорода x граммов
Возьмем 3-процентный раствор перекиси водорода y граммов
В первой порции содержится чистой перекиси водорода 0,3x
Во второй порции содержится чистой перекиси водорода 0,03y
Всего в двух порциях содержится чистой перекиси водорода 0,3x + 0,03y
Смешаем обе порции (x + y) граммов
В смеси должно содержаться чистой перекиси водорода 0,12(x + y)
0,3x + 0,03y = 0,12(x + y)
Что же это за алгебраический объект у нас получился? Попробуем дать ему название.
(уравнение) (с двумя переменными)
3. Формулирование темы и целей урока.
Это линейное уравнение с двумя переменными.
Сформулируем тему урока. (Линейное уравнение с двумя переменными)
Чтобы вам хотелось узнать сегодня на уроке?
(Что называется линейным уравнением,
Что называется решением уравнения с двумя переменными,
Свойства линейного уравнения)
4. Актуализация базовых знаний с совместным постижением нового материала. Нам ведь уже знакомы похожие объекты? Что это за объекты? (линейные уравнения с одной переменной)
Давайте придумаем какое-нибудь линейное уравнение с одной переменной. Пожалуйста, к доске (вызвать 3-4 желающих)
-Посмотрите на доску, перед нами действительно линейные уравнения с одной переменной. Вспомним общий вид линейного уравнения с одной переменной. (ax=b, где a и b –некоторые числа, а x-переменная).
Выпишите номера тех уравнений, которые бы вы отнесли к линейным уравнениям с двумя переменными? (1,4,6) (со слайда презентации)
1. 3у+2х=0.
2. 5у – 6 =0.
3. 0,2х2 – у +3=0.
4. х+у=15.
5. 4х – 17 = 0.
6. 5х+2у=12
Выпишите номера тех уравнений, которые бы вы отнесли к линейным уравнениям с двумя переменными? (1,4,6)
Определим вид линейного уравнения с двумя переменными: (ax+by=c, где a,b,c некоторые числа, x, y переменные.)
Попробуйте сформулировать определение:
(Линейным уравнением с двумя переменными называется уравнение вида ax+by=c, где a,b,c некоторые числа, x, y переменные)
Откройте теоретический справочник. Прочитайте определение про себя. Не ошиблись ли мы в определении. Есть ли различия?
Придумайте и запишите в этом справочнике свое линейное уравнение с двумя переменными.
Вернемся к линейным уравнениям с одной переменной. Давайте вспомним, как они решаются, и решим какое-нибудь из придуманных уравнений с объяснением, например:
2х+6=10
(Перенесем слагаемое без х в правую часть уравнения, изменив при этом его
знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе
части уравнения на 2, получим х=2).
- Ребята , такие уравнения вы хорошо умеете решать.
- А какие свойства применяли при решении этих уравнений? (Если в уравнении слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.)
- А какое еще свойство вы применяли? (Если разделить или умножить обе части уравнения на одно и тоже отличное от нуля число, то получится уравнение равносильное данному.)
Линейные уравнения с двумя переменными обладают такими же свойствами.
Применяя эти свойства, будем получать равносильные уравнения. Напомните, пожалуйста, какие уравнения называются равносильными? (Уравнения, имеющие одни и те же решения, называют равносильными. Уравнения, не имеющие решений, также считают равносильными.) Для уравнений с двумя переменными все остается в силе.
Загляните опять в справочник.
Ребята, ведь мы забыли про мастеров из парикмахерской. Это не хорошо. Надо им помочь. Давайте вернемся к той ситуации. Применим свойства уравнений с двумя переменными к полученному нами уравнению, и сведем его к виду, указанному в определении.
0,3x + 0,03y = 0,12(x + y)
0,3x + 0,03y = 0,12x + 0,12y
0,3x – 0,12x = 0,12y – 0,03y
0,18x - 0,09y =0
18x - 9y=0
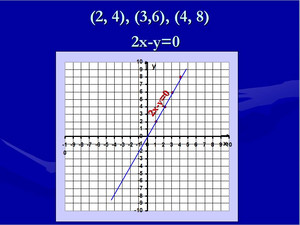
2x-y=0
При каких значениях x и y наше уравнение обратится в верное равенство?
при х=1, у=2 (записываю на доске) (2∙1=2)
Что же является решением линейных уравнений с двумя переменными? (Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.)
Прочитайте это определение на странице про себя. Не ошиблись ли мы, давая определение?
А какие еще пары чисел будут являться решениями уравнения 2x-y=0?
х=2, у=4
х=3, у=6
х=4, у=8
Правильно решениями этого уравнения будут являться числа, одно из которых в два раза больше другого.
Т.е 3-процентного раствора надо взять вдвое больше, чем 30-процентного. Как же смешать? (дети показывают на практике) мерить будем мерным стаканчиком.
Продолжим знакомство с линейными уравнениями.
Присмотритесь, пожалуйста, к этим парам. Может есть у кого предложение, как записать это решение короче, пользуясь символическим языком математики?
( (2, 4), (3,6), (4, 8) и т.д.)
-При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой – на втором. В записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у.
Где-то нам уже встречалась такая запись! Правильно, это координаты точек на координатной плоскости.
Отметим на координатной плоскости найденные пары решений.
Есть ли еще у нашего уравнения решения? Сколько же у него решений? (бесконечно много)
Можем ли мы все его решения нанести на координатную плоскость? (да, они образуют прямую) Все ли решения будут пригодны для ситуации в парикмахерской?
Сделаем вывод о количестве решений линейного уравнения с двумя переменными (множество решений уравнения с двумя неизвестными, как правило, бесконечно и его изображение на координатной плоскости — прямая линия, а также может быть и пустым)
Всегда ли именно прямая линия?
-Рассмотрим уравнения 5х+2у=12.
-Для удобства нахождения решений уравнения, воспользовавшись свойствами уравнений, выразим из этого уравнения одну
переменную через другую, например у, через х. Для этого перенесем
слагаемое 5х в правую часть уравнения изменив его знак.
2у= -5х+12.
-Разделим обе части этого уравнения на 2:
у= -2,5х+6
Уравнения 5х+2у=12 и
у= -2,5х+6 – равносильны.
-Пользуясь формулой у=-2,5х+6, можно найти сколько угодно решений уравнения
5х+2у=12. Для этого достаточно взять произвольное х и вычислить
соответствующее ему значение у.
Например: если х=2 , то у= -2,5.2+6=1.
если х=0,4 то у= -2,5*0,4+4=5.
Пары чисел (2; 1), (0,4; 5) – решение уравнения 5х+2у=12.
Это уравнение имеет бесконечно много решений.
Этот способ удобен и тогда, когда надо найти не все, а только несколько решений уравнения, причем каждый раз можно выбирать, какую переменную выражать через другую.
Рассмотрим уравнение
2x+0y=13
Построим его график: x=6,5
Рассмотрим уравнение
0x+3y=15
Построим его график:
y=5
5. Подведение итогов. Спасибо вам за общение. Мне понравился полет ваших мыслей. Понятен ли вам язык алгебры?
-Какой вид имеет линейное уравнение с двумя переменными ? (ах+ву=с).
-Что называется решением линейного уравнения с двумя переменными ?
-Приведите примеры таких уравнений.
-Какими свойствами обладают уравнения с двумя переменными?
|

