Тема урока: Скрещивающиеся прямые.
Учебная тема: Взаимное расположение прямых в пространстве
Предмет: математика (геометрия)
Класс: 10
Учебник: Геометрия, 10-11: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.- М.: Просвещение, 2014.
Цель урока: Ввести понятие скрещивающихся прямых. Доказать признак скрещивающихся прямых.
Конспект урока
Цель:
Ввести понятие скрещивающихся прямых. Доказать признак скрещивающихся прямых.
Задачи:
1. Познакомить учащегося с возможным расположением прямых в пространстве.
2. Способствовать развитию мыслительных процессов: обобщение, систематизация; развитие памяти, аналитического и логического мышления.
3. Способствовать формированию умения рационально использовать рабочее время, адекватной самооценки.
Метод:
Репродуктивный: при решении задач и выполнении самостоятельной работы по готовым чертежам.
Частично-поисковый: при ответе на вопрос самостоятельной работы.
Продуктивный: при доказательстве признака скрещивающихся прямых (найти другой
способ доказательства)
Оборудование: Компьютер, онлайн доска, макеты параллелепипеда и пирамиды.
План урока:
- Организационный момент. (2мин)
- Актуализация опорных знаний. (4 мин)
- Определение темы урока, целей. (1 мин)
- Изучение нового материала. (14 мин)
- Закрепление нового материала. (14 мин)
- Проверка знаний. (4 мин)
- Домашнее задание. (2 мин)
- Итоги урока. (4 мин)
Ход урока.
Учитель определяет готовность учащегося. Проверка домашнего задания.
Актуализация опорных знаний. Определение целей и темы урока.
Вопросы учителя:
- Какие случаи расположения прямых в пространстве ты знаешь?
- Какие прямые называются параллельными?
- Назови признак параллельности прямых в пространстве.
- Какие прямые называются пересекающимися?
Задача: Дан параллелепипед АВСDA1B1C1D1
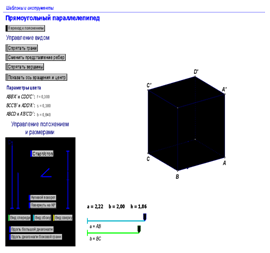
По рисунку определите расположение в пространстве прямых
- АВ и СD, (прямые параллельные)
- DD1 и СD, (прямые пересекаются в точке D)
- АD и KF. Постройте точку пересечения этих прямых.
- АВ и C1D1, (прямые параллельные)
- ВС и KF. Постройте точку пересечения этих прямых
- АВ и DD1 (прямые не пересекаются и не параллельные).
Учитель: Такие прямые называются скрещивающимися.
Учащемуся предлагается сформулировать тему и цели урока.
Изучение нового материала.
Дается определение скрещивающихся прямых.
| Определение: Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. |
Вывод: Сколько возможных случаев расположения прямых в пространстве можно выделить?
Три:
- Лежат в одной плоскости и пересекаются;
- Лежат в одной плоскости и не пересекаются;
- Лежат в разных плоскостях и не пересекаются.
Демонстрация примеров.
| Две прямые в пространстве могут |
| Лежать в одной плоскости |
|
Не лежать в одной плоскости |
| в этом случае они могут |
|
тогда они называются |
| пересекаться |
не пересекаться |
|
| |
|
|
|
| Пересекающиеся прямые |
Параллельные прямые |
|
Скрещивающиеся прямые |
Задание: В онлайн доске на рисунках параллелепипеда и пирамиды показать пары скрещивающихся, пересекающихся и параллельных прямых.
Доказывается признак скрещивающихся прямых:
| Теорема: Если одна из двух прямых лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются. |
Доказательство:
Рассмотрим прямую АВ, лежащую в плоскости α, и прямую CD, пересекающую эту плоскость в точке С, не лежащей на прямой АВ.
Докажем, что АВ и CD – скрещивающиеся прямые, то есть они не лежат в одной плоскости.
Метод от противного (ученику предлагается самому дописать части доказательства)
1. Допустим противное:
2. Тогда:
3. Противоречие:
4. Вывод:
Доказывается теорема:
| Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна. |
Доказательство:
Рассмотрим скрещивающиеся прямые АВ и СD.
Докажем, что через прямую АВ проходит плоскость, параллельная прямой СD, и такая плоскость только одна.
- Проведем через точку А прямую АЕ, параллельную прямой CD, и обозначим буквой α плоскость, проходящую через прямые АВ и АЕ.
- Прямая CD не лежит в плоскости α и параллельна прямой АЕ, лежащей в этой плоскости. Следовательно прямая CD параллельна плоскости α.
- Плоскость α – единственная плоскость, проходящая через прямую АВ и параллельная прямой CD. В самом деле, любая другая плоскость, проходящая через прямую АВ, пересекается с прямой АЕ, а значит, пересекается и с параллельной ей прямой CD.
Теорема доказана.
Закрепление нового материала.
Задача №1. Через вершину А ромба АВСD проведена прямая а, параллельная диагонали BD, а через вершину С - прямая b, не лежащая в плоскости ромба. Докажите, что а) прямые а и CD пересекаются; б) а и b - скрещивающиеся прямые.
Задача №2 (резерв) . Докажите, что если АВ и CD скрещивающиеся прямые, то AD и ВС также скрещивающиеся прямые.
Проверка знаний.
Учитель предлагает проверить свои знания по теме:
Точка D не лежит в плоскости треугольника АВС, точки M, N, P - середины отрезков DA, DB, DC соответственно, точка К лежит на отрезке BN. Выясните взаимное расположение прямых:
а) ND и AB
б) РК и ВС
в) MN и AB
г) MP и АС
д) KN и АС
е) MD и ВС
Оценка:
6 заданий – «5»
5 заданий – «4»
4 задания – «3»
Домашнее задание: п.7, определения, теоремы учить.
Задача: На рисунке изображен куб. Докажите, что прямые:
а) АА1 и В1С1
б) A1D1 и DC
в) АС и ВD1 - являются скрещивающимися.
Подведение итогов урока. Рефлексия.
Литература:
- Геометрия, 10-11: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.- М.: Просвещение, 2009.
- УМК «Живая математика». Компьютерные альбомы. Институт новых технологий.

